|
对数学基础的0和1的新认识 本著刊发在《中国科技纵横》2016年01期 陆道渊著 书眉:客观存在是无悖的;理学中悖论,必是人的错误认识造成的。 摘要 发现并使用“实数”新概念,消除了理学中一切有关的重大悖论(请注意:学术研究中的矛盾一词,实质上分两种概念,必须要分清:1、一个命题自我否定,简称悖,必错;2、两个命题的互相否定,哪个错未确定。所以命题有 悖 就自我否定而不成立。)和疑难,并展示了消悖实例,使数学、理论物理学彻底浅简了 。 关键词: 总段1、〈自然数〉、〈量数〉、〈整数〉等。 学习和研究数学、物理学的人都知道,现行理学中有很多重大悖论和疑难;连逻辑主义数学家弗雷格也说‘逻辑在哪里出了毛病呢?很多人百思不得其解。这一问题直接威胁到数学的基础………更重要的是,威胁到自然数的定义。’,还说‘对什么是1这样一个貌似简单的问题,尚未有一个完满的答案……否则,我们最终将弄不清楚负数、分数或复数。’(引自[3]) 数学家们也都哀叹数学的悖论灾难越来越深重了;有些数学家试图用“零(记为0)和无限大(记为∞)是关于1的反演点,即0∞=1”的方法(引自[1]的8页)来躲避如影随形的悖论,但更不通了,因为现行的所谓“实数”已(无理的)规定“0是整数、偶数,但不能做除数”;而且0既然是“实数轴”的始点,而∞却在无限的遥远,也不是真正的反演。明摆着,是“实数”有毛病,即“实数轴”为无限的直线是错误的。 令人惊喜的是,如把“实数轴”改为有限的线段,则整个现行数学基础就被革命性纠正,从而所有相关的悖论和疑难也随之全部消除。 于是,所谓“实数”就有了其新概念〈数〉 (用〈〉 表 示 新概念)。 一、“实数”的新概念 先取“实数轴”的正半轴射线改为线段 ,再把它有限等分,并把有序性编号①、②、③…从左向右标在相应的分点上,则1、2、3…等称为有序积段,而①、②、③…是其分点的 编号,如图1。对这同一线段,当有序编号增大,则等分分段△n间隔缩小(符号△专使△n≡1),如图2。  



  
图2显示出四点: 第Ⅰ、总 段(总段用粗体1标志,以区别于积段1)的始点是;是0的编号; 第Ⅱ、如果反序读正半轴的  ,则也出现负号,这说明正负符号与有序积段  本身无关(例如钱这数量,其本身是没有正负的,只在使用时才出现正负。); 第Ⅲ、如把每一分段△n继续不断十等分,则  ,但≠,否则△n=1/=0,总段就不存在了,这 就 有 悖 ;这证实了不属于总 段 1,即和分别属于 1和∞而在两者界点的编号。所以编号为的∞不在总段上,而 是 总段1的终端之外的空间。注 意 , 同一界点的两个编号和是不容许换位的;但现行的“实数轴”是无限的射线,才使数学家们把和合二为一了,即可以=了,这是“实数”有缺陷的根本原因; 第Ⅳ、不管编号如何增多,恒有△n=1,即等分分段△n≡1。 
  
        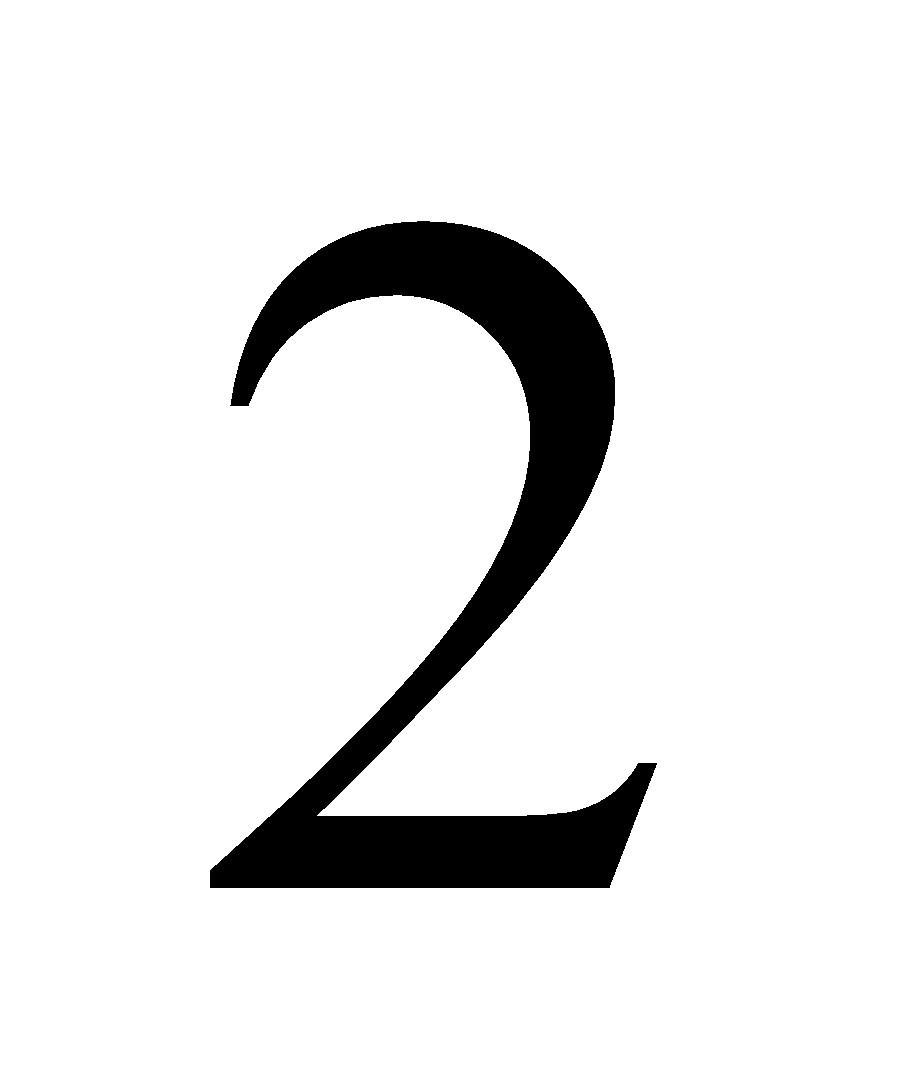
      同理,现用的负半“实数轴”用上述办法也可显出这四点,如图3。 然后把图2、 图 3在点连接成一条线段,就成了一条完整的 新 数 轴, 如图4。当无轴排序时,才在编号前加负号表示左序。显然整个新数轴仍以总段1标出,其分段编号为两组。总段1的两端之外都是∞了,也即,两端点都是n与∞的界点,都标着和两个编号,很容易把和混同为一,请看图4)。 由四个图可知,0是不真的数,因为它没有长度,因此0在新概念中仅表示‘无’、‘空位’等。由图4可看出,0是微观的‘无’,∞是宏观的‘无’,作为数都是不真的。要有总段1,才能被有限多的编号等分后得到有限多的有序积段  ;如果没有总段1,就会把有序编号误认为就是有序积段n; 据上述知,把 总段1按有序编号等分后,各从始点到的点的有序积段  称为〈自然数〉 ;但 这〈自然数〉  是有限的,所以是新概念,其数轴是新概念数轴。 注意:事实上总段1不是〈自然数〉的1,因为它不是由等分得到,因而没有编号,所以不是数。 不连续的〈自然数〉叫〈整数〉。所以〈整数〉中没有正号、负号和不真的数0、∞ 。 数学范畴不能引入各种量,因而没有量纲(量纲即量度单位),以致人们不会区别〈纯数〉和〈量数〉两个概念,现在有了新概念〈自然数〉,就可区别〈纯数〉和〈量数〉了,例如 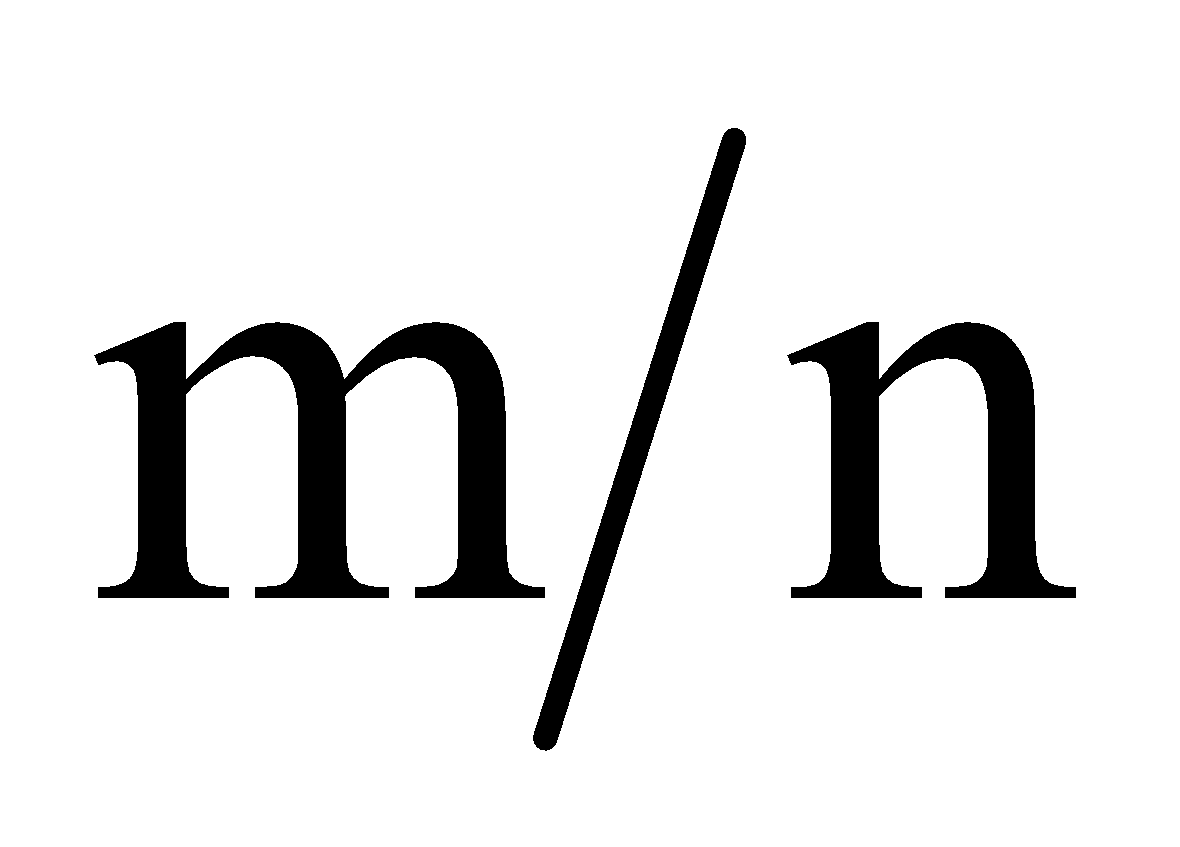 和m /,虽然两者都是〈自然数〉之间关系性式子的数,但前者是〈纯数〉而后者是〈量数〉。 进而,一切小数无论是‘有理的,无理的,或超越的’,实质上都是物理元素间或几何元素间的关系的值,亦即仅由〈自然数〉  (是其编号)间按各种 关系 性 运 算 符号 组成的式子产生,如 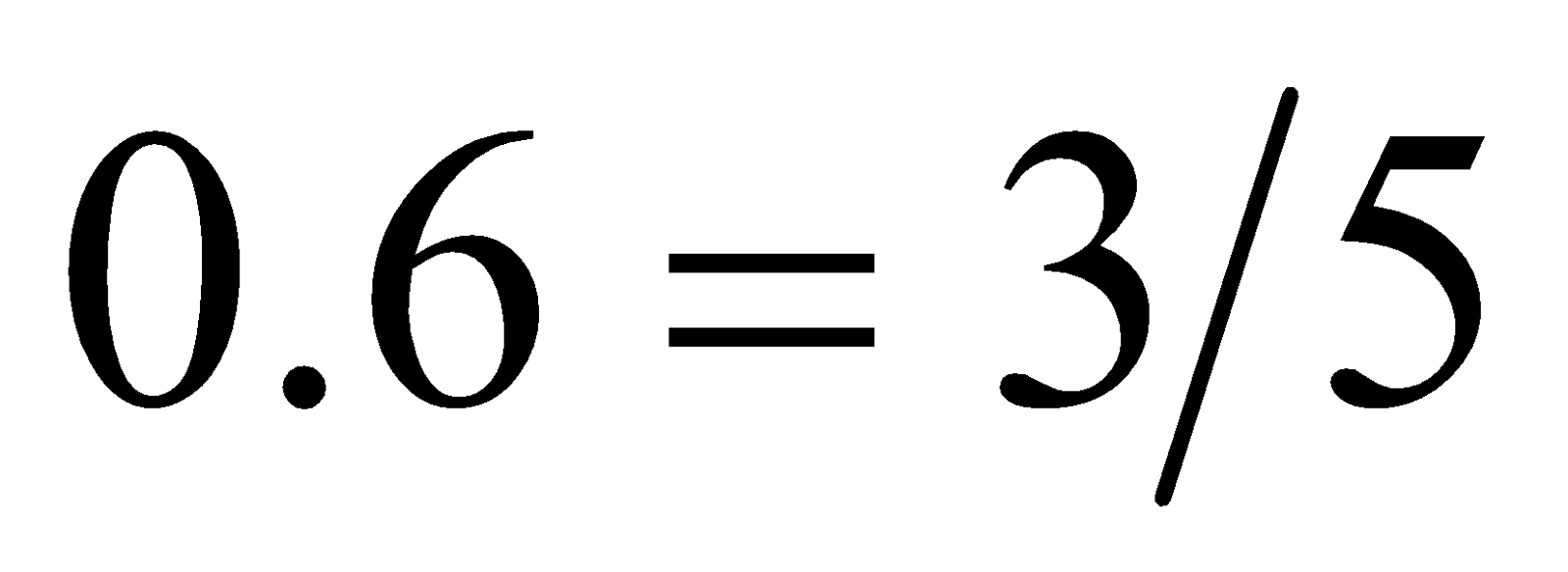 、  、1.4142……= 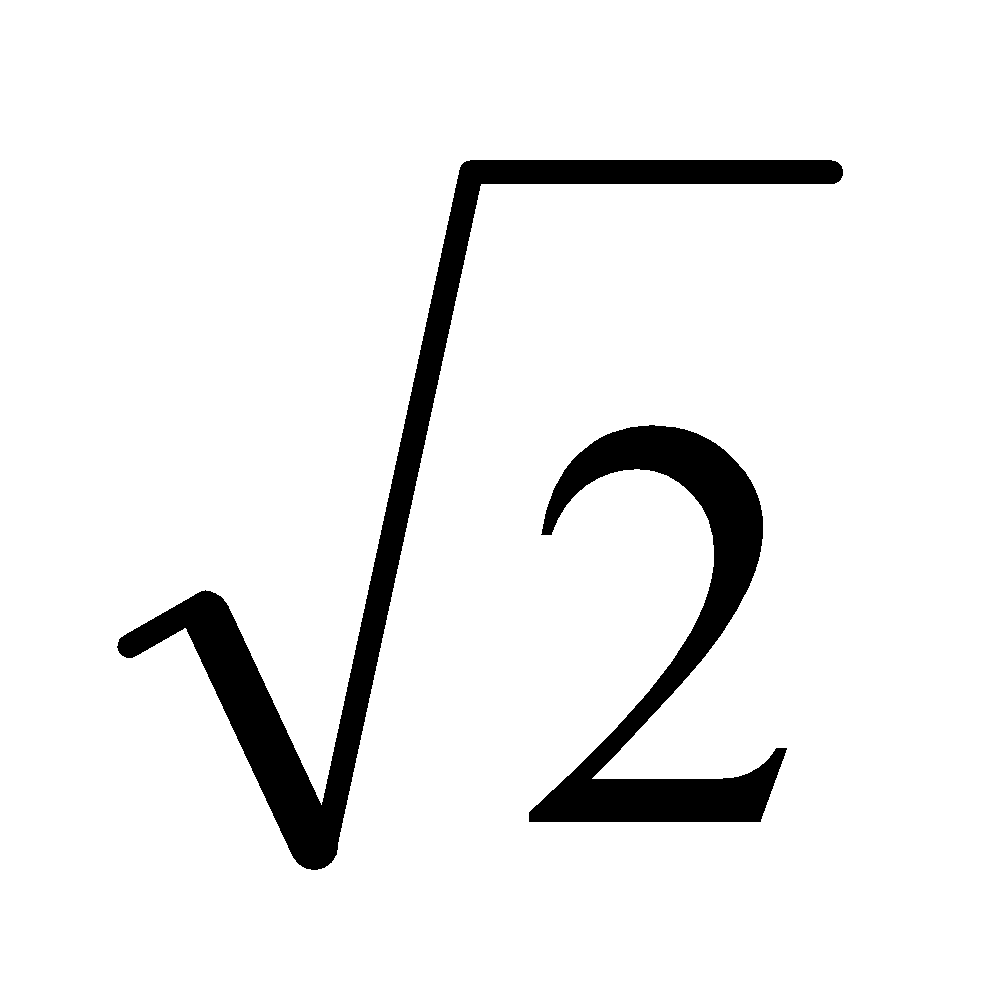 、  =  【注意,在没有量纲的条件下, L,D都只能是 ( 存 在 性 的 )〈整数〉 ,不可能是(关 系 性 的 )小数;因为总可以用最小的度量单位,能使小数点消去。】、 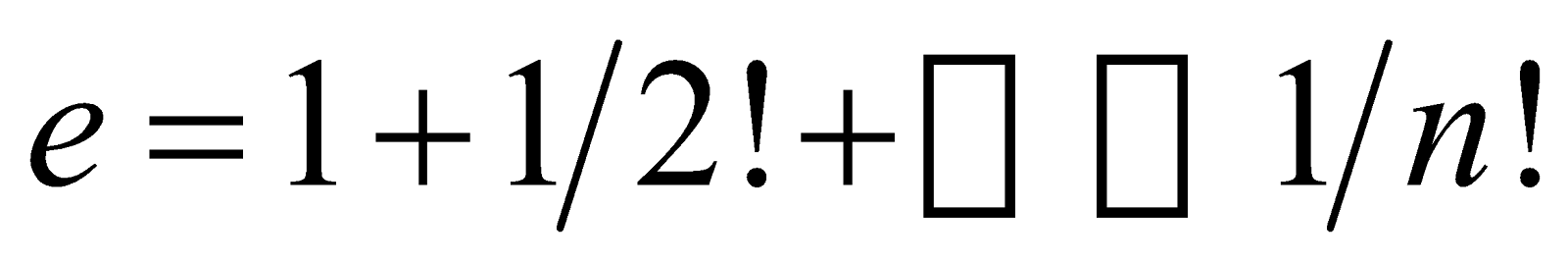 ,等。 有了 新概念〈自然数〉,就 知 道 任何小数在表达上都没有独立性(须由〈自然数〉组成的式子表出),而 且 甚 至没有完全性(如无限小数须取近似值),所以都不能标在新 概 念 数 轴上。有了〈自然数〉,还 容易区分无限小数中的“无理性和超越性”,如无限小数、无理数 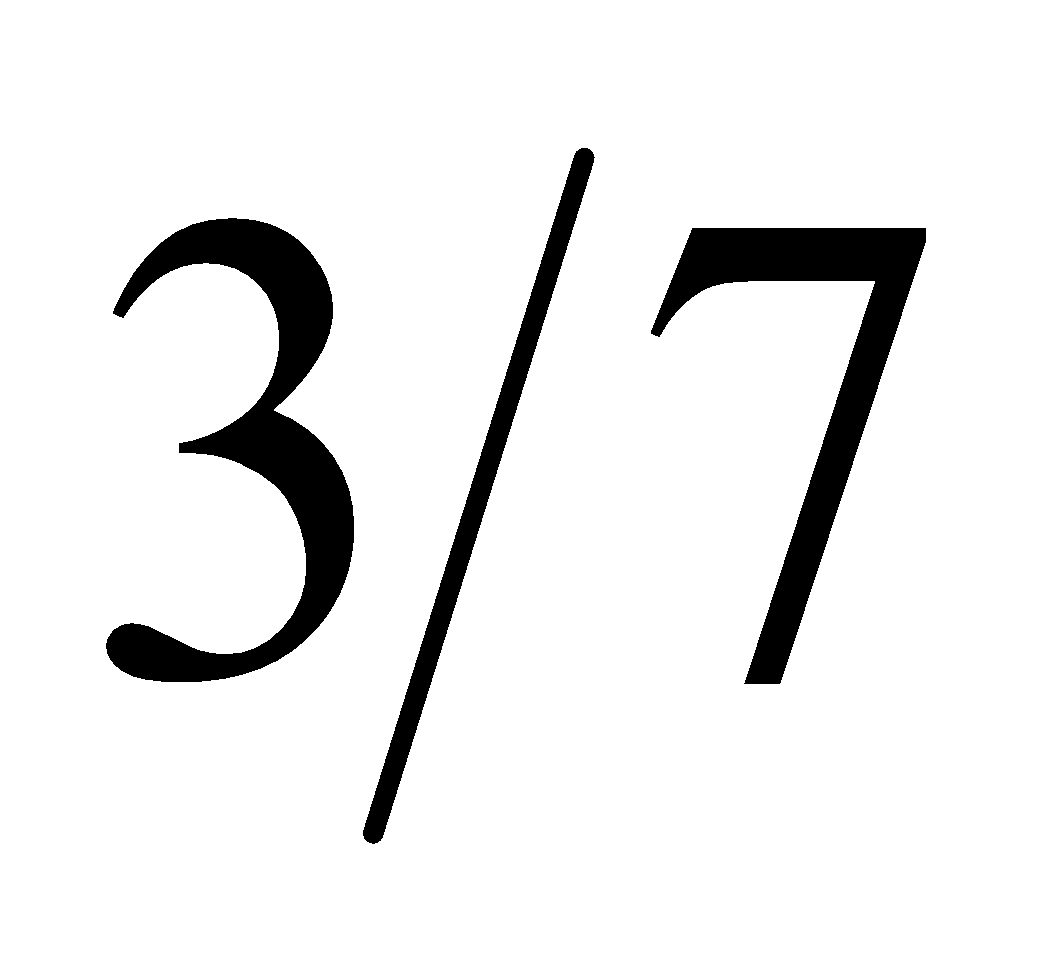 、 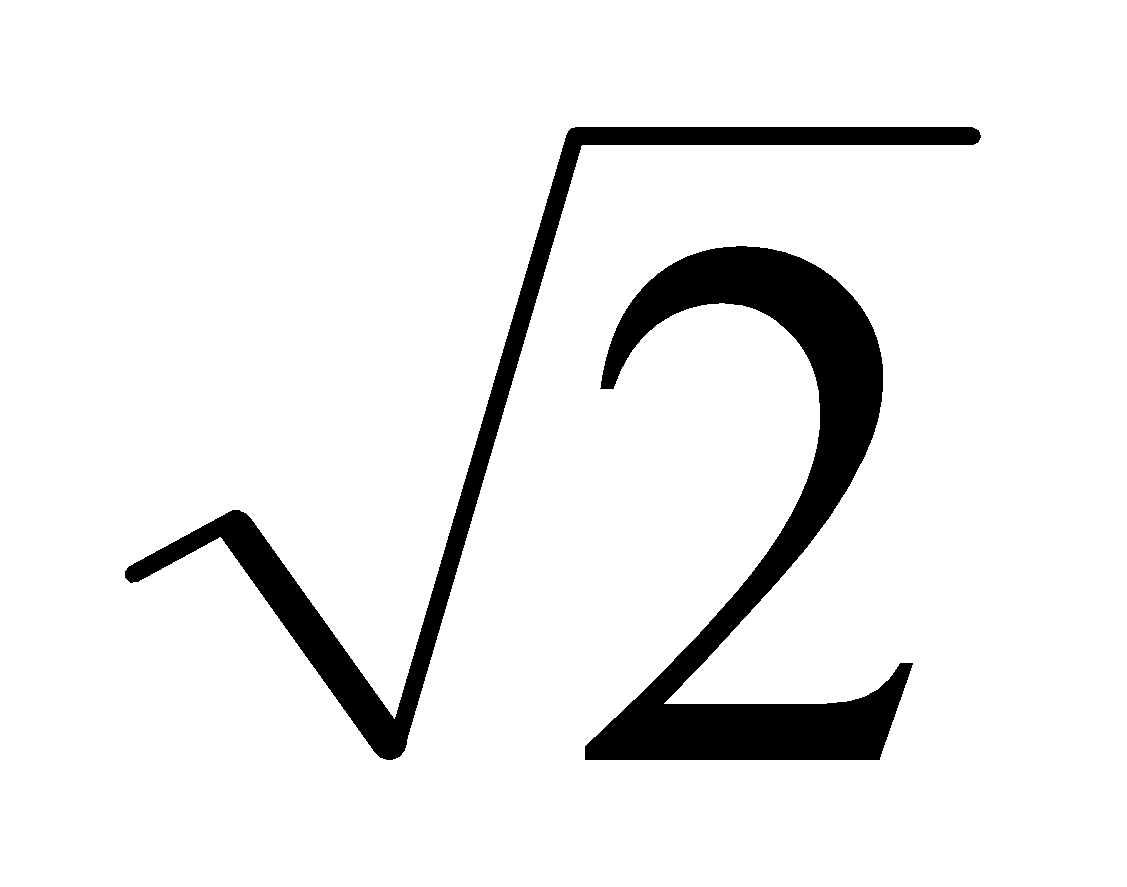 这两式中的 〈整数〉 是确定的,而  、  中〈整数〉 是不确定 的,这就是  、  为何具有‘超越性’的原因。显然,这一判断方法是简明有效的(而康托的用数轴判断法是错误的,因为凡小数都是关系性的数,在数轴上是没有的)。 由新 概 念 数 轴可看出,<整数>n表示‘有限大’,其编号表示‘有限多’;同理,0表示‘无大’, 其编号表示‘无多’,∞表示‘无限大’, 表示‘无限多’。这就证实了,数学家们为躲避悖论所用的“0和∞是关于1的反演点,即1/0 →∞”,须纠正为用新概念表达的1/=才正确,因为和分别是总段1的两个端点,1才是真正的‘反演段’(不是“反演点”;请参看图4);这与上面论证相印证。 上面已证实,正负号是附着〈整数〉的而不是含在其中的,于是可得虚符: 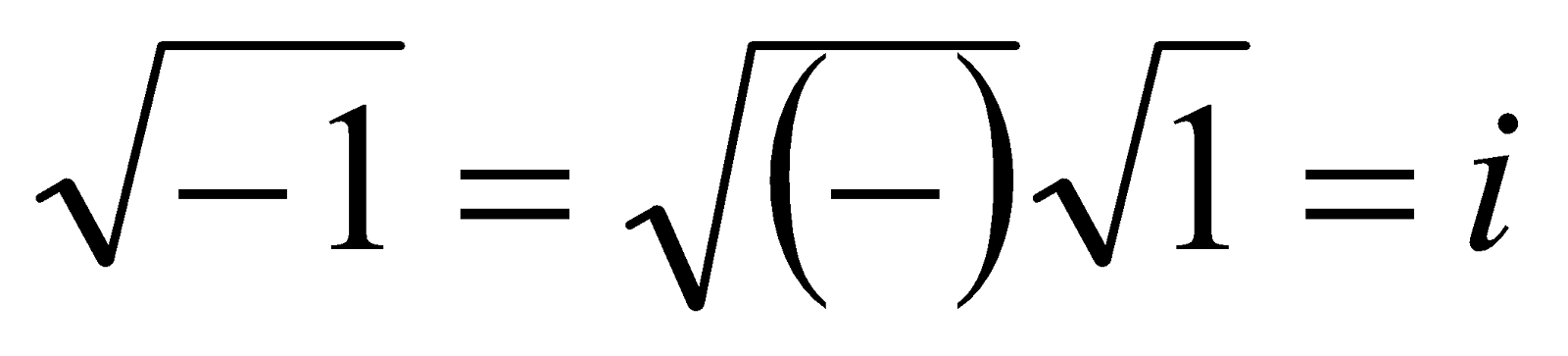 ,从而 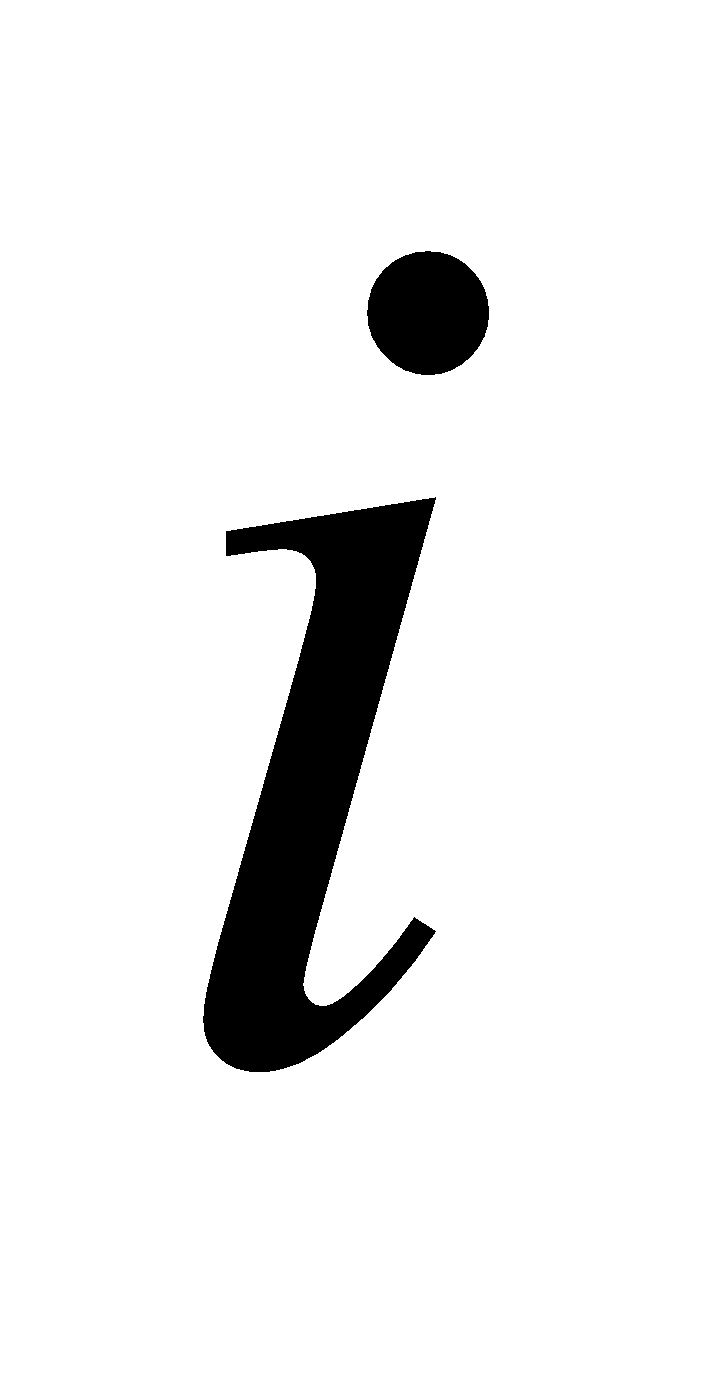 也是附着〈整数〉而不是含在其中的,所 以‘虚数’实 质 是〈虚符〉,仅起隔开、过渡和连接的作用,如‘复数’ a+ 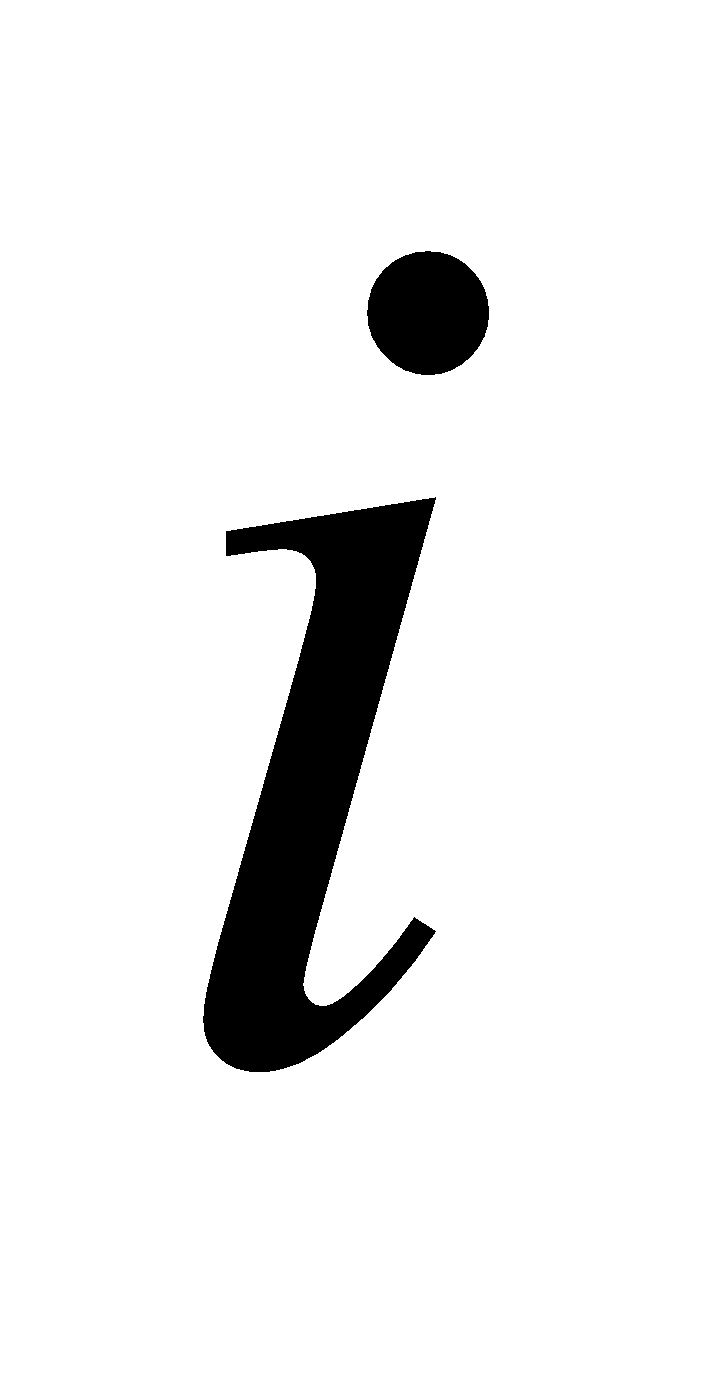 b,实质是两〈整数〉 a和b由〈虚符〉 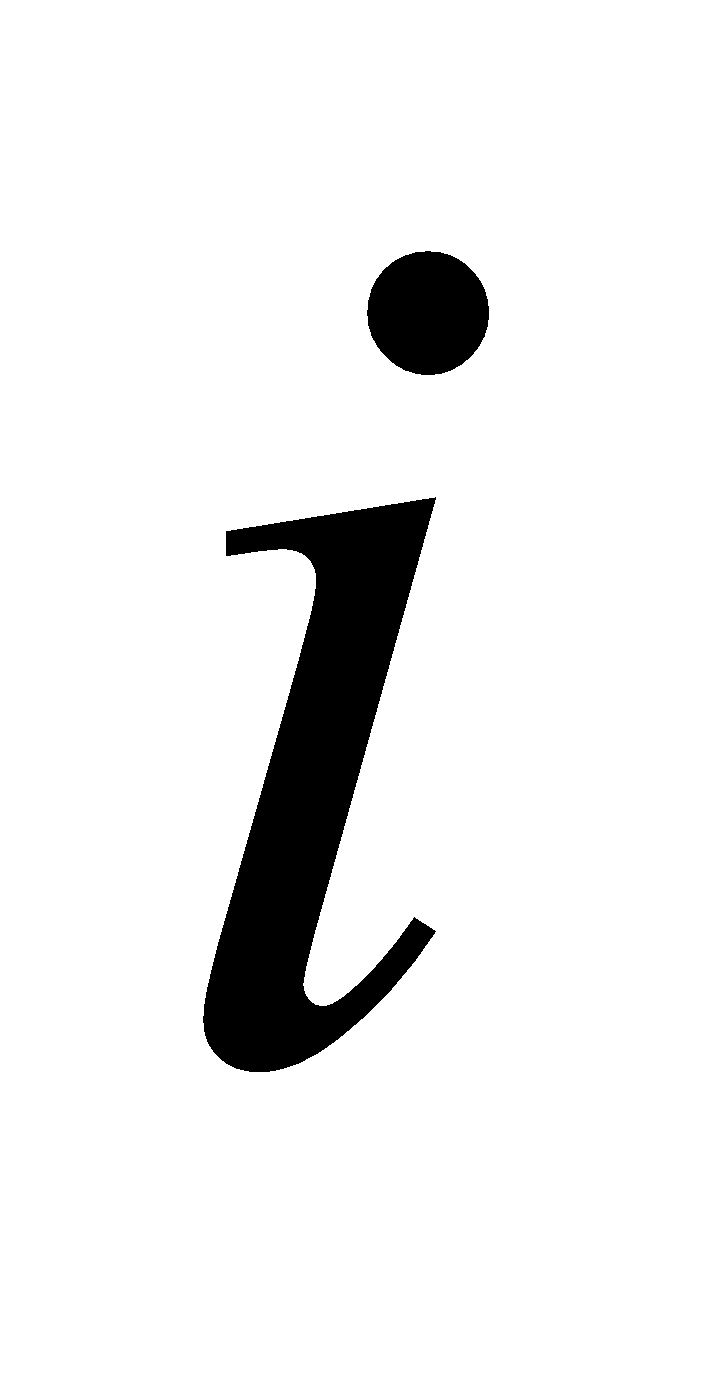 连接而成。 概 括上 述 ,总 称 为“实数”的含义不合事实,应改称为〈数〉,表示新概念:〈数〉包括由总段1所产生的真的数〈自然数〉  和其编号、不真的数0、  和其编号、,和由〈自然数〉  和其编号按各种关系 性 运 算 符号 组成的式子产生的各种小数。用〈虚符〉连接的〈数〉可依旧称为‘复数’。 最后,还须提醒四点: 第Ⅰ、既然在新概念的数轴上,不存在各种小数,所以还证实了与“实数”相关的所谓“开区间”、“闭区间”也是假概念,由新概念编号取代,,这极大的浅简了高等数学。 第Ⅱ、函数关系性(不管是几何关系或是物理关系)的数,不是坐标轴(坐标轴由数轴组成)上本身所有的存在性的数。所以,坐标轴上,只能标上存在性的数即新概念〈自然数〉;当 用到不同函数式的分数、小数和无理数时,只能临时在轴上点出。 第Ⅲ、上述证实了,客观只存在‘线段’,即‘线段’是真概念,而‘射线’和‘直线’应分别是‘一个端点暂未确定的线段’和‘两个端点都暂未确定的线段’的简称。 第Ⅳ、由1/0=,从而有1/=  ,这证实了0 是微观的‘无’,∞ 是宏观的‘无’;‘无’即‘空间’, 1表示总‘物质’ ;这表达了宇宙有限和无限的统一。 二、解决现行数学中几个已公认无法解决的悖论和疑难的实例 【现在有了“实数”新概念〈数〉,解决这些悖论连初中生都可轻松看懂】 1、“整体等于其局部”悖论和对其解决: 现行科教书依据所谓“实数”,用康托的“一一对应法和势的大小”证出“自然数与其正偶数(或正奇数)一样多”,从而得出“整体等于其局部”。 解决:由于新概念〈自然数〉是有限的,即知这是悖论。 2、“康托集”悖论和对其解决: 现行科教书关于“康托集”的表述是(引自[2]363页和366页):“把区间 [0,1](即长度为1的线段)三等分,弃中间子区间(1/3,2/3);如此连续弃中,问弃的数多还是剩的数多?”,“经运算,所弃的子区间之和的长度A=1;但还剩点集X,其元素(即长度为零的点)有无穷多;用一一对应法,点集X的元素与长度A中的元素一样多”;“与我们的习惯思维似有矛盾……全部区间都扔掉了,但像没扔掉。” 上面引文显示,编著者实际已承认了其“证明”是悖论;事实上,所弃的和还剩的都不是“点集”而是‘段集’(即其元素都是长度不为零的小线段)。 解决:用新概念〈自然数〉,所谓“区间 [0,1]”(注意,有了〈自然数〉的‘编号’,“区间”已被‘编号’取代,即所谓“开区间”、“闭区间”已被否定)实即总段1,其终点编号≠,即所弃的“子区间”总长度为A,而所剩的区间之和的长度为a;所以A远大于a。于是该悖论解决。 3、“连续统假设”悖论和其解决: 现行科教书已承认了该“假设”是无法解决的第一难题。 解决:由新概念〈自然数〉知,该“假设”是“整体等于其局部”悖论的一般化,这等于已得到解决。 4、罗素悖论的解决: 罗素在研究自然数时发现了罗素悖论:‘集包含自身为元素’。第三次数学危机由该悖论的提出引起;至今没有解决。 解决:如用新概念的〈自然数〉,因总段1不是积段的1,即总段1不是〈数〉,就不会‘集包含自身为元素’,于是 罗素悖论即得解决。 5、‘费马大定理(xn+yn=zn,当n>2时,无正整数解)’疑难的解决: 现行科教书依据现行“实数”概念,宣称该‘定理’由怀尔斯在1995年成功证明,但数学家们都认为怀尔斯的证明太冗长、不浅简,因而其证明性不强(注意,费尔马在关于这不定方程的待求正整数解这页的空白处写道:‘…………我已发现了这个美妙证法,可惜这里的空白地方太小,写不下。’ ;这证明费尔马的‘美妙证法’是很简短的。) 如用新概念〈自然数〉,可简洁证明如下: 首先,应把费马定理式子重新写成x+y=z,这是因为由“实数”新概念,指数只能是以<整数>为底数的编号。由于自然空间只能是三维的(因为过自然空间中一点只能引两两互相正交的三条直线。),所以当>,该定理式子的x、y、z就都不成线段,从而就不存在,所以没有<整数>解;当=、=,已知有<整数>解;当=,人们已证没有<整数>解。所以当>时,x+y=z无<整数>解。证毕。 所以,失逸的费尔马的‘美妙证法’,必是这种证法。 6、现行教科书中两个疑似已解决的著名悖论(即‘庄子悖论’和‘芝诺悖论’,请看[1]的第3和第9页), 其实并没有真的解决,原因就是没有积段n和分点编号之分,即虽知  ,却 不 知 ≠,把和两个编号混同了,才说出“无限段路程之和可以是有限量”(引自[1]的第3页末;注意,此话是具体、清楚的低劣错误,出于数学家之口,实为数学的悲哀)这种有悖的“结论”,从而没能真正解决这两个悖论。所以,只有知道新概念<自然数> n是有限的,即  但≠,表达了仅具‘未知性’而不具‘无限性’,从而不会把与混同(由图4更可直观看出,总段1的终点是n与∞的界点,并标着、,很容易混同),才使这两个著名悖论得到真正的彻底解决。 所以,这实例6,应概括为一句直观而浅简的实质性表述:总段的n是积段,而每分段恒为1,于是有n÷1=,这编号就有限;当此确定线段被长度为0除,有n÷0=,即得编号等于;于是和都不在此线段上而分处总段的两端(和分别是n与∞ 分界点的编号,看图4);所以区分了n和,这两著名悖论才彻底解决。 (为简,更多实例,略。) 显然,使用“实数”的新概念<数>,能消除悖论而没有不良副作用。 参考文献: [1]《话说极限》.张景中主编 梁昌洪编著 书号为ISBN 978-03-023788-0 科学出版社出版. [2]《数学聊斋》(第二版).张景中主编 王树禾编著 书号为ISBN7-03-013958-5.科学出版社出版. [3]《当代英美哲学举要》.赵敦华编著.书号IBSN7-80092-552-8 当代中国出版社出版. 悖论自由研究者 陆道渊 [url=mailto  DY247484@126.com]LDY247484@126.com[/url]
|